Study of
letter serial correlation (LSC)
in some English, Hebrew,
Aramaic, and Russian texts
1. Measurement and calculation
By Brendan McKay and Mark Perakh
Posted October 20, 2009
Contents
1. Introduction
2. Letter Serial Correlation effect. Measurement and calculation
3. Calculation of the expected serial correlation sum
4. Calculation of the expected serial correlation density
5. Approximate estimate of the expected correlation sum for n=1
6. Approximate calculation of the expected correlation sum for arbitrary n
Meaningful texts consist of paragraphs (or verses), sentences, words, and at the most
basic level, of letters. To convey a meaningful message, all this elements of a text must
be placed in a certain order, prescribed by the language's grammatical rules and by the
specific contents. As a result, each meaningful text is highly structured, comprising many
levels of order superimposed upon each other in a complex manner. The complexity of a
text's structure is assured by the enormous number of possible combinations of letters,
words, sentences etc.
A general measure of the text's degree of disorder vs order is its entropy.
Having determined the entropy of a text provides only a generalized idea of the degree to
which the text is not random. Different types of information could be extracted from texts
by unearthing specific forms of order present in a text and by trying to connect them to
the semantic peculiarities or to the meaning-bearing contents of texts. Any information
obtained in that respect seems to be of interest if one wishes to understand such a
complex and extremely important phenomenon of human's existence as language.
The subject of this paper emerged as a side topic in the course of investigation of the
Bible code controversy [1-4] which largely deals with the so called ELS (Equidistant
Letter Sequences) found in abundance in the Bible, as well as in any non-Biblical
texts. While it is hard to indicate the direct connection of the above controversy to the
effect described in this paper, the effect in question seems to be of interest in its own
right, and, moreover, some connection to ELS, which is not obvious at this time, may well
be found later.
To avoid introducing any new terminology when it is not dictated by the requirement of
clarity, in the following parts of this paper we will use word "text" both for
meaningful texts, such as that of the Book of Genesis, or L. Tolstoy's novel War and
Peace, etc, and for any random collection of symbols, including those obtained by
permuting letters of the original meaningful text, even when these collections of symbols
(in our case letters of alphabets) constitute a gibberish without conveying any meaningful
contents.
One of the many types of order found in texts is what we will refer to as Letter Serial
Correlation (LSC), and this paper reports on a study of that type of order in some
English, Hebrew, Aramaic, and Russian texts. Its essence is as follows.
Let us denote the total number of characters in the text by L. We divide the
text into k segments of equal size n=L/k. These segments will be
referred to as chunks. The total number of occurrences of a specific letter x
in the entire text will be denoted Mx . Let the numbers of
occurrences of letter x in any two adjacent chunks, identified by serial numbers i
and i+1, be Xi and Xi+1 . We will be
measuring and calculating the following sum taken over all letters of the alphabet (i.e.
for x varying between 1 and z where z is the number of letters
in the alphabet) and over all chunks (i.e. for i varying between 1 and k):
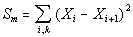 ...........................................(A) ...........................................(A)
In this study, the measurement of the above sum was performed using a computer program
which divided the text into various numbers k of equal chunks, counted the
numbers of each letter in each chunk, and calculated expression (A). If the division
of the text into k chunks resulted in the last chunk (chunk # k) to be
incomplete, i.e. having less letters than the rest of the chunks, such residual incomplete
chunk was cast off and not accounted for in expression (A).
If the total number of complete chunks in the text is k, there are k-1 boundaries between the chunks, and since the pairs of adjacent
chunks's overlap, there are k-1 pairs of chunks. The summation
is performed both over (k-1) pairs of chunks and over all z letters of
the alphabet. If a certain letter is absent in both adjacent chunks, the term in sum
(A) corresponding to that letter and to the pair of chunks in question is
zero.
Consider the particular case of chunks having size n=1. In that
case the number of chunks in the text is k=L, where L is the
total length of the text. Chunks of that size can contain only one letter each. Therefore
the terms in sum (A) in that case can only be either 0 or 2. The zero value happens in two
possible situations. One is when some two adjacent chunks contain the same letter
x. In this case the term in sum (A), corresponding to letter x and to that
pair of chunks, becomes zero. The other situation is when some letter x is
absent in both of any two adjacent chunks. Then the term in sum (A) corresponding
to x and to that pair of chunks also becomes zero. If one of
the adjacent chunks contains letter x, and its neighhboring chunk contains another letter
y, then both x and y found in that pair of chunks contribute to sum (A) equal terms of 1,
so the total contribution to sum (A) of that pair of chunks is 2. Therefore the
maximum possible value of sum in (A) is Sm=2(L-1), which happens if no two
adjacent chunks contain identical letters. If n>1, the maximum possible value of
the measured sum will be correspondingly larger, and its calculation is more
complex. What is of interest though is not the maximum possible value of sum (A) but
its expected value, which we will calculate precisely for texts randomized by
permutations.
If all the chunks contained exactly equal numbers of each letter, then obviously we
would find that Sm= 0. The actual behavior of Sm , in particular in
its relation to the calculated "expected" sum, and in comparison to its behavior
in randomized texts, would indicate the presence of a certain type of order in the tested
texts. Unearthing the features of such order is the goal of this study.
To analyze the behavior of the measured sum in the real meaningful texts, we need to be
able to compare it with the behavior of the expected sum Se,
calculated on the assumption of the text being a randomized conglomerate of z
letters, each letter having the frequency of its occurrence in the randomized text exactly
equal to its frequency in the real, not randomized, meaningful text.
We have to distinguish between perfectly random texts and texts randomized
by permutation of a specific initial text.
The text, which has been randomized by a permutation of the letters of a specific
initial text, contains the same letters as the original text, with the same
letters' frequency distribution. It means that every letter x which happens
Mx times in the original text (which also may be referred to as identity
permutation) will happen the same Mx times in every random permutation of
the letters of the original text. Depending on the composition of the original text, the
numbers of occurrences of each letter will be different for each original text but the
same in all of its random permutations.
There can be, rarely, a situation, when a certain letter is absent in the original
text, and then it will be also absent in all of its permutations. A good example is the
novel titled A Story of Over 50000 Words Without Using Letter E, by E.V. Wright,
published in 1939 by Wetzel Publishing Co of Los Angeles. Letter E is the most frequent
one in English (as it is also in German and Spanish). E.V. Wright managed though to write
a novel 267 pages long without using letter E even a single time. Obviously, any random
permutation of the text of that novel would not contain letter E either.
A perfectly random text is different. In a perfectly random text each letter
of the alphabet has the same chance to appear at any location in the text, and in a
sufficiently long text the letters frequency distribution is uniform.
The following section contains the derivation of a formula for the calculation of the
expected sum Se , based on the assumption that the text in question has been randomized
by permuting its letters. (For perfectly random texts the formula
would need to be slightly modified).
Considering the distribution of values of X we have to make choice between multinomial
and hypergeometric distributions [5]. The first one, being an extension of the binomial
distribution, pertains to tests with replacement, while the second one, to the tests
without replacement. In our case the stock of letters available to fill up a chunk is
limited to the set of letters contained in the identity permutation. After letter x
has been picked for a chunk, there is no replacement for it available in the stock of
letters when the second letter is to be picked (which does not mean that the second letter
cannot be identical with the first one, but only that the choice of letters becomes more
restricted with every subsequent letter to be plucked from the stock). Therefore our
situation is obviously meeting the conditions of tests without replacement. Hence, we
postulate hypergeometric distribution of X, being identical for chunks i
and i+1 as the chunks are of the same size.
Since the sizes of all chunks (in the same test) are identical, we have
Var(Xi) = Var (Xi+1)...................................(1)
and
E(Xi)=E(Xi+1), ...........................................(2)
where Var(X) denotes variance and E(X) denotes expected value of X
[5].
Step 1. Variance is determined by the following formula of Math. statistics
[5, page 175]:
Var (X) = E(X2) - [E(X)]2...........................(3)
The first term on the right side of eq. (3) is the expected value of squared X and the
second term is the squared expected value of X.
Consider expression E[(Xi+Xi+1)2] i.e. the expected
value of a squared sum of Xi and Xi+1.
Applying formula (3) we have
E[(Xi+Xi+1)2]=Var (Xi+Xi+1) + [E(Xi+Xi+1)]2..................(4)
From Mathematical Statistics [4] the expected value of a sum equals the sum of expected
values of its components. Accounting also for eq. (2), we obtain from (4):
E[(Xi+Xi+1)2]=Var (Xi+Xi+1) + 4[E(Xi)]2...........................(5)
Now consider expression
E[(Xi-Xi+1)2] + E[(Xi+Xi+1) 2].........................................(6)
Replacing the sum of expected values with the expected value of the sum and accounting
for eq.(2) we get from (6)
E[(Xi-Xi+1)2]
+ E[(Xi+Xi+1)2 = E[(Xi-Xi+1)2
+ (Xi+Xi+1)2] =
= E[(Xi2+Xi+12-
2XiXi+1+ Xi2+Xi+12+2XiXi+1]=
=E[2Xi2+2Xi+12] =E[4Xi2]
= 4E[Xi2]...................(7)
Now subtract eq (5) from eq (7):
[(Xi-Xi+1)2] = 4E[Xi2]
- 4 [E(Xi)]2 - Var (Xi+Xi+1)..............(8)
From eq. (3) we see that the first two terms in the right side of (8) equal 4Var[Xi].
It yields
E[(Xi-Xi+1)2] = 4Var[Xi] -Var [Xi+Xi+1]..................(9)
Comment: 1) If the text under consideration were a perfectly
random one, then Xi and Xi+1 would be independent variables.
Our text is though not a perfectly random one, as defined earlier in this paper,
but a text randomized by permutation. In a perfectly random text, every letter of
the alphabet is equally available to fill any site in that text. In a text randomized by
permutation only those letters are available to fill up the chunks which are present in
the original text, and in specific numbers Mx. Therefore, if chunk #i contains
more of a letter x, it diminishes the available stock of that letter x for chunk #(i+1).
Hence, there is a certain negative correlation between Xi and Xi+1,
which means these two numbers are not independent variables. Therefore variance of the sum
Xi+Xi+1 cannot be replaced with the sum of variances [5]. Var (Xi)
and Var(Xi+Xi+1) in formula (9) must be calculated separately and
then substituted into (9). If though Xi and Xi+1 were
independent variables, i.e if we assumed that the text was perfectly random, then the
right side of equation (9) would reduce to 2Var(Xi).
Step 2.
In the case of a hypergeometric distribution the formula for variance is as follows [6,
page 219]:
Var(Xi)=(L-m)mp(1-p)/(L-1)..........................(10)
where p=Mx/L, and in our case, for the first term on the right side
of (9) the sample size m1=n where n=L/k, k
being the number of chunks in the particular text, and n being the size of a
chunk. L is the total number of all letters in the entire text, and Mx
is the total number of occurrences of character x in the entire text. For the
second term on the right side of (9), the sample size is m2=2n=2L/k.
Then :
4Var [Xi] = 4 (L-L/k)(1-Mx /L)Mx/k(L-1),
or, after an elementary algebraic operation,
4Var[Xi}=4Mx(L-Mx)(1-1/k)/k(L-1)..................(11)
Similarly, replacing L/k with 2L/k we obtain for the second term in (9)
Var(Xi+Xi+1)=2(1-2/k)Mx(L-Mx)/k(L-1)...............(11a)
Finally, substituting (11) and (11a) into (9) we obtain
E[(X-Xi+1)2]
= 2Mx(L-Mx)/k(L-1)........................... (12)
The next step on the way to calculating the serial sum Se is
summing up expressions (12) for all pairs of chunks and for all letters of the alphabet.
Since all chunks in the same test have the same size and the distribution of each letter
is identical for all chunks, the summation over all pairs of chunks can be effected simply
by multiplying expression (12) by k-1, which is the number of pairs of chunks in
the text. Then the final formula for the calculation of the expected serial sum is as
follows:
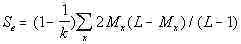 ..................(13B) ..................(13B)
Comment: * If Xi and Xi+1
were independent variables, i.e. if we assumed that the text was perfectly random, the
distribution of any X within a chunk would be approximated by a binomial distribution (as
a marginal distribution of a multinomial one) rather than by a hypergeometric
distribution, since in a perfectly random text the stock of available letters is
unlimited. It would make our case analogous to tests with replacement. The
actual calculation (which we omit here) shows that using the variance for a binomial
distribution yields a formula which differs from (13B) only by a factor of (L-1)/L.
Since the text's lengths in our study were typically minimum tens of thousands letter
long, the quantitative difference between formula (13b) and that for a perfectly
random text turns out to be utterly negligible. *
For each value of k the summation in (13) is performed over all letters of the
alphabet, accounting for the actual numbers Mx of occurrences of each
letter in the tested text.
Since k=L/n, where n is the size of a chunk, equation (13B) can be
rewritten as an explicit function of chunk's size n:
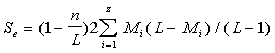 ............(13C) ............(13C)
Comments: a) The sum in formulas (13B) and (13C) contains as many terms as there are
various letters in the text. With a very few exceptions, texts usually contain all letters
of the alphabet, although in different numbers Mx. Therefore, the sum in (13)
almost always contains z terms, where z is the number of letters in the
alphabet.
b) Theoretically, equation (13C) appears to be one of a straight line in Se-n
coordinates, with the intercept
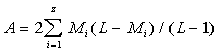 ....................(14) ....................(14)
and the negative slope
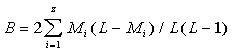 .....................(15) .....................(15)
An equation in the form Se=A-Bn describes a straight
line starting at Se=A when n=0 and dropping to zero at n=L.
However, quantities A and B are actually not constant for the following reason. In
actual calculations, the text is divided into k chunks, each of size n.
For n=1 always k=L. However, already for n=2 two
different situations are possible. If the total number L of letters
in the text is even, then for n=2, k=L/2, and the total length L
of the text in formula (13C) is the same L as for n=1. If,
though, L happens to be an odd number, the last chunk is a residual one,
containing only one letter instead of n=2. In this case the last chunk is
cast off, both when calculating Se by formula (13) and when measuring Sm in
accordance with formula (A). Then in formula (13C), instead of L, the
quantity of L-1 is used. This may also change by 1 the quantity Mi
for one of the letters. Hence, in the case of an odd L, the intercept
A and the slope B become slightly different for n=2 compared to n=1.
Analogously, for each value of n, the last chunk may happen to
have fewer letters than n, and such a chunk is cast off. For example, the
Book of Genesis in Hebrew comprises 78064 letters. Then, if the chunk's size is
chosen to be n=1, the number of chunks will be k=78064. For
chunk's size of n=2 the number of chunks will be k=78064/2=39032, and
the overall length of the text is L=78064, which is the same as for n=1.
However, if the chunk's size is n=3, the number of chunks appears to be k=78064/3=
26021.333. The number of chunks cannot be fractional, therefore for n=3 the
number of chunks must be taken as k=26021, casting off the last, incomplete
chunk, whose size is 0.333 of a complete chunk. This means truncating the text,
whose length L in formula (13) will be replaced by L*=26021*3=78063
instead of L=78064. This changes the values of the intercept A
and slope B in equation (13).
The variations in the values of A and B are different
for various values of n. When the size of a chunk is measured in thousands,
the last, incomplete chunk may be substantial in size (for example, if the size of a chunk
is chosen to be 10000, the amount by which the text is truncated can be as large as
9999 letters). In Table 1, as an example, the values of L* are shown for
the text of the Book of Genesis, as a function of the chunk's size n. This table
illustrates the variations in the texts' lengths, used for calculation of Se
and for measurement of Sm, which occur because of the text's
truncation.
Larger size of the cast off chunk does not necessarily translate into a larger
variation of A and B, since simultaneously with the decrease of L
(due to truncation) also the values of Mi for some letters decrease,
thus softening the overall variation of A and B.
Table 1. Actual texts' lengths L* as a function of n and k.
L=78064, Genesis, Hebrew
| > n |
> k |
> L* |
1 |
78064 |
78064 |
2 |
39032 |
78064 |
3 |
26021 |
78063 |
5 |
15612 |
78060 |
7 |
11152 |
78064 |
10 |
7806 |
78060 |
20 |
3903 |
78060 |
30 |
2602 |
78060 |
50 |
1561 |
78050 |
70 |
1115 |
78050 |
100 |
780 |
78064 |
200 |
390 |
78000 |
300 |
260 |
78000 |
500 |
156 |
78000 |
700 |
111 |
77700 |
1000 |
78 |
78000 |
2000 |
39 |
78000 |
3000 |
26 |
78000 |
5000 |
15 |
75000 |
7000 |
11 |
77000 |
10000 |
7 |
70000 |
Now let us introduce the Letter Serial Correlation density. First we introduce the expected
density de, and later we will likewise introduce the measured
Lettter Serial Correlation density dm. To calculate the expected
density, we modify formula (13C) by dividing it by n, thus defining the expected
Letter Serial Correlation density de as the expected
LSC sum per one letter in a chunk:
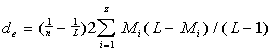 ..............(16) ..............(16)
which is an equation of a hyperbolic curve for a quantity de+T=dt
which is
dt=de+T=(Q/n)......................................(17)
where the constants are
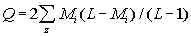 ...........................(18) ...........................(18)
and
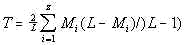 ............................(19) ............................(19)
In log-log coordinates equation (17) is represented by a perfect straight line. It
starts at n=1 where de=Q-T and is dropping toward de=0
at n=L (since T=Q/L). Note that curves for de and
dt are at a distance of T from each other along de
axis, but in log-log coordinates both curves, for de and dt
, have the same slope. In the actual calculations the straight line for eq. (17) in
log-log coordinates will necessarily be slightly distorted because of the truncation of
texts described earlier in this paper. A formal representation of the
distortion in question can be given by modifying equation (17) as follows:
de=dt-T= Q[(1/(nq)]-T...........................................(20)
where the power is q=1 for the ideal dt-n hyperbole, but q
is slightly different from 1 for real, almost hyperbolic curves, the
deviation of q from 1 being caused by the texts' truncation effect. In
the following sections of this paper we will see how well equation (17) is obeyed by
real de=dt-T curves. The curves for de
will serve as reference measures for the measured densities dm
which are measured LSC sums per one letter in a chunk.
Both expected and measured Letter Serial Correlation densities are introduced in a way
analogous to that commonly used in Thermodynamics for such quantities as, for
example, chemical potential which most often is chosen to be Gibbs potential per one
particle (or per one mole). While Gibbs potential is an extensive quantity, the
chemical potential is an intensive one. Using that intensive (as all specific
quantities are) variable often enables one to reveal some fundamental features of a
phenomenon. Likewise, in our case both expected and measured sums are
extensive quantities, while the expected and measured densities are intensive. For
the interpretation of experimental data, both extensive and intensive parameters have
their appropriate places. As it will be demonstrated later in this article, considering
both types of quantities allows for a more compete analysis of experimental results than
if discussing the total sums alone.
While the value of Se varies for various texts, it is possible to
roughly estimate the expected value of that sum as a function of the text's
total length, L, without using the precise formula (13). This can be done
in a rather simple, even if a quite approximate way, for the simplest case when the
chunk's size is n=1, so that the number of chunks in the text is k=L
where L is the total length of the text. For this approximation we assume
that the distribution of all letters is uniform, i.e. that Mx , which is
the number of occurences of letter x in the text, is equal for all letters.
First note that each pair of adjacent chunks i and i+1 can contribute
to the sum only one of two values, namely either 0 or 2. If the text under
exploration contained spaces between words, the following situations would be possible. 1)
letter x is found neither in chunk i nor in chunk (i+1).
Then the term in the sum corresponding to letter x in that pair of chunks is 0
(even though that pair of chunks may contribute a non-zero term due to a letter other than
x). 2) Chunk i contains letter x and chunk i+1
contains a space, so it is empty. In that case the term in the sum contributed
by that pair of chunks is 1. 3) Both chunks i and i+1 contain
either identical letters other than x, or spaces. In that case the term in the
sum corresponding to letter x in that pair of chunks contributes 0 to the sum
(even though that pair of chunks may contribute either 0, 1 or 2 due to letters other than
x). 4) Chunk i contains letter x and chunk i+1
contains some other letter y. In this case the pair of chunks in
point contributes 2 to the sum, as both x and y contribute 1 each.
In our case, though, spaces between the words are ignored. Therefore each
chunk contains some letter, and there are no empty chunks. Hence, case 2, and
consequently contribution of 1 by any pair of chunks with n=1 is impossible. Thus
the terms in sum Se , for n=1, can be only either 0 or 2.
Pick an arbitrary chunk i and assume that it contains letter x. What is
then the probability px that in the adjacent chunk there is again the
same letter x? In a random text, the probability of any letter to occupy any
location is px=Mx/L where Mx is the
number of occurrences of letter x in the entire text. Since one letter x
is already occupying the chosen chunk i, the probability that the adjacent chunk i+1
also contains the same letter x is (Mx-1)/(L-1). The
texts subjected to study all contained at least tens of thousands of letters. Since
Mx is roughly between twenty and thirty times smaller than L,
the values of Mx in the explored texts all were at least several
thousands letters large. Then a good approximation is the replacement of (Mx-1)
with Mx and (L-1) with L. The probability that the
chunk adjacent to i contains a letter other than x is then 1-Mx/L.
Hence, there is the probability of Mx/L that the corresponding term in
the sum for Se is 0 and the probability of 1-Mx/L that the
term in point is 2. Now, assume that all letters of the alphabet appear in our text
with the same frequency, which then equals M=L/z, where z is the total
number of letters in the alphabet. In this case, there is a probability of 1/z that
the term contributed to the sum by any two adjacent chunks is 0 and the probability of
1-1/z that the term in question is 2. In such a text the expected number of
chunks of 1 containing non-identical letters is then L(1-1/z). Then the expected
value of the sum is Se=2(L-1)(1-1/z) while its maximum possible
value is 2(L-1) which of course is the same as for the measured sum.
For example, in an English text 100000 letters long, accounting for z=26 for English,
we find the expected sum, in the case of chunks having n=1, to be: Sm1=2(100000-1)(1-1/26)=198385.
Then Se/L=1.903. Similar calculation for various languages and text lengths
shows that the ratios of the expected sum to the text length, for n=1, usually fall
between 1.6 and 1.92, their mean value being about 1.85. More precise calculation for
specific texts in English, Hebrew, Aramaic, and Russian, for n=1, using formula
(13), produced numbers between 1.55L and 1.87L, their mean value being about 1.8L.
It is possible to reasonably estimate the value of Se, starting
from formula (13C) and assuming that all z letters in the text have the same
frequency which then will be M=L/z for each letter. {This assumption
is of course wrong, as it is tantamount to the suggestion that the expected value of
expression Mi(L-Mi) in formula (13C) equals M(L-M).
The expected value of a product equals the product of expected values only for independent
variables [6, page 173] while M and L-M are obviously not independent
from each other}. However, as we will see, quantitatively, our
assumption that the mean value of Mi(L-Mi) equals M(L-M)
provides for the values of Se which are reasonably close to the actual
values determined by formula (13C)}.
We rewrite formula (13C) replacing Mi with M, and, hence
replacing the sum in it with the product z.M(L-M). Accounting for M=L/z:
Se= (1-n/L) 2 zM(L-M)/(L-1) = (1-n/L) 2z (L/z)(L-L/z)/(L-1) =
= (1-n/L)2L2(1-1/z)/(L-1).................(21)
This is an equation of a straight line in Se-n coordinates with the
intercept of
A=2L2(1-1/z)/(L-1)...................................(22)
and the negative slope of
B=2L(1-1/z)/(L-1)......................................(23)
That straight line drops to zero at n=L.
Let us compare the results obtained by equations (21)-(23) to the values of Se
calculated by precise formula (B).
For example, for the Book of Genesis in Hebrew L=78064, z=22, then
the intercept is
A=2 . 780642 (1-1/22)/(78064-1)= 149033.
The value of Se at n=1 is Se(1)=A(1-1/L)=
149033(1-1/78064)=149031.
For n=10 Se(10)=149033(1-10/78064)=149013.
Using formula (B), the corresponding values are Se(1)=145121, and Se(10)=145097.
The discrepancy for Se(1) is (149033-145121)/145121=0.026 i.e about 2.6%
The discrepancy for Se(10) is (149013-145097)/145103=0.026 i.e. also about
2.6%.
If we created artificially a text containing equal numbers of each letter (and also in
absence of a text's truncation) formula (21) would be the precise one for that text.
If accounting for truncation, that formula could be made precise for the text in question
by replacing the nominal text's length L with its truncated length L*.
(Such a text has been created indeed for the study of some effects not covered in
this report. This topic is discussed in separate papers at Letter serial correlation (LSC) in additional languages and various types of texts and Letter serial correlation in additional languages).
f) It follows from the derivation of formula (13C) that the expected serial sum Se
is averaged over all possible permutations of letters in the tested text. On the
other hand, the measured sum Sm is found in each measurement as a
value for that particular text. Therefore, even if the test is performed on a version
randomized by permuting letters of the original meaning-bearing text, the measured sum Sm
will necessarily differ from the calculated, averaged expected sum Se.
Of course we expect that for randomized texts the difference
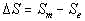
will be limited to reasonably small fluctuations around zero value. This our
expectation will be verified experimentally.
As to the non-permuted meaningful texts, finding and analyzing the difference between
the expected sum Se and the experimentally measured sum Sm
is one of the specific goals of the experiment in point.
The experimental results obtained for various texts are described in the second
and in the third parts of this report (see
Experimental results -- randomized texts
and Experimental results -- real meaningful texts) and their discussion and interpretation are offered
in the fourth part (see http://members.cox.net/marperak/Texts/Serialcor4.htm
).
References
1. D. Witztum, E. Rips, and Y. Rosenberg, Statistical
Science, 1994, v. 9, No 3, 429-438.
2. B. McKay et al. Web postings at http://cs.anu.edu.au/~bdm/dilugim/.
3. M. Perakh et al. Web posting at http://members.cox.net/mkarep/.
4. List of references to Bible-code-related publications at http://www.answering-islam.org/Religions/Numerics/index.html.
5. R. J. Larsen and M. L. Marx. An
introduction to Mathematical Statistics and its applications. Prentice-Hall
Publishers, 1986.
6. M. Dwass. First Steps in Probability.
McGraw-Hill Co., 1967.
Originally posted to Mark Perakh's website on February 9, 1999.

|


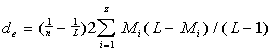 ..............(16)
..............(16)![]() ...........................(18)
...........................(18)![]() ............................(19)
............................(19)![]()

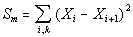 ...........................................
...........................................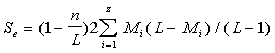 ............
............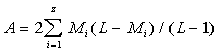 ....................(14)
....................(14)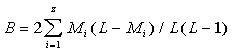 .....................(15)
.....................(15)